Discover what foods work for you
Let yourself be guided by our experts and your wellness goals will be within reach.
Take the quizIt’s quick and free.
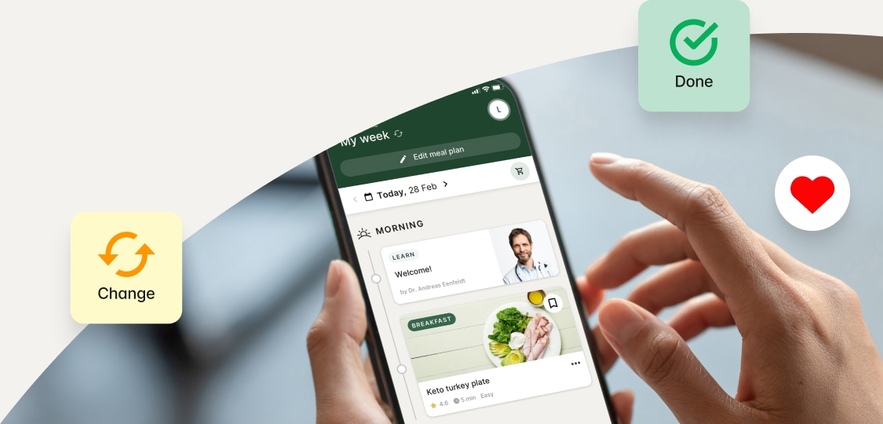
How it works
You tell us your goals.
We’ll help you get there.

Take the quiz
The free quiz only takes a few minutes.

Get your personalized plan
We’ll create a meal plan that matches your preferences and needs.

Take it one step at a time
Our expert guidance keeps you on the right track.
Is it for me?
You deserve
a better health journey
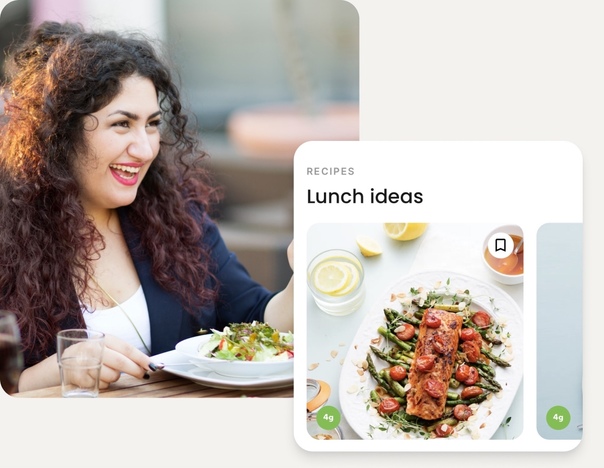
Personalization means made for you
We’ll guide you to the delicious foods that will help you meet your goals. Whether you’re trying to manage type 2 diabetes or looking for help with weight loss, we can guide you toward the meals that make success easier.
Enjoy life without hunger, cravings & struggle
When you find the food that’s right for you, everything gets easier. Say goodbye to hunger, and welcome a quieter feeling: satisfaction. Many members say their cravings fell away when they stopped dieting and started eating better.


Stay confident — you’re on the right track
Our app helps you visualize your journey to better health with daily tips, tracking, recipes, and education. Follow along through our expert-led practical guides about anything and everything — from budgeting, to navigating social situations, and much more!
Meet the experts
We aim to provide unbiased guidance rooted in evidence-based information, nutritionally-reviewed recipes that satisfy, and inspiring tools to help you reach your goals in a sustainable way.
Customizable approach. Lasting results.
You’ll find success doing it your way, not our way. Expect a science-based approach that you’ll enjoy — and results you’ll love.
What to expect
Guidance at your fingertips
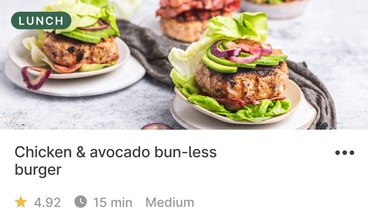
Discover the food that works for you
Use our recipes, meal plans, and smart shopping list, or learn to put together easy meals from restaurants or takeout. Wherever you eat, we’ll help you find the best options.

Knowledge is power
Learn about more than just food. Understand some basic nutrition science, and get helpful tips about forming new habits. Our courses, guides, and videos have it all.

Expert support is key
Questions and bumps in the road will pop up. Our community of members and experts are here with answers and inspiration. Find the support you need, and help others, too.
600+ success stories
Real people. Real results.
Take the quiz
And start your
journey with us
Get started now













